DiedergruppeDefinition 'DiedergruppeC''
Universität
Es sei E die reelle euklidische Ebene und 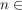 . Es sei . Es sei  (siehe symmetrische Gruppe) die Drehung um den Winkel (siehe symmetrische Gruppe) die Drehung um den Winkel 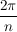 und s die Spiegelung an der y-Achse. und s die Spiegelung an der y-Achse.
Die von d und s erzeugte Untergruppe
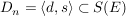
heißt die Diedergruppe 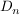 . .
Man sieht:
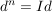 , ,
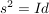 , ,
dsd=s.
Da die von d und s erzeugte Untergruppe aus allen endlichen Produkten von d, 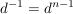 und und 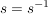 besteht, sieht man mit den obigen drei Regeln, dass jedes Element von besteht, sieht man mit den obigen drei Regeln, dass jedes Element von 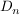 von der Form von der Form
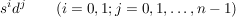
dargestellt werden kann. Es gilt also:
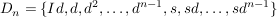 . .
Also hat 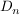 die Ordnung 2n. die Ordnung 2n.
Quelle: isbn3446130799
|