DifferenzenquotientSei 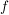 eine Funktion, die über dem Intervall eine Funktion, die über dem Intervall 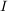 definiert ist, und sei definiert ist, und sei 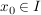 . .
Dann nennt man
den Differenzenquotienten der Funktion 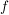 zur Stelle zur Stelle 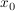 . .
Bildet man den Grenzwert des Differenzenquotienten für 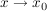 , dann erhält man den Differentialquotienten: , dann erhält man den Differentialquotienten:
Beispiel:
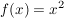
Differenzenquotient: 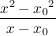
Wegen 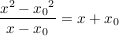
kann man in diesem speziellen Fall den Grenzwert sogar durch unmittelbares Einsetzen von 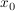 für für  ermitteln: ermitteln:
Alternative Schreibweise ("h-Methode")
Manchmal ist eine andere Schreibweise hilfreich:
man setzt 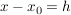 , also , also 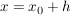
Damit wird der Differenzenquotient zu:
der Differentialquotient lautet analog:
|