EinführungAnalysisHier entsteht eine Sammlung von Aufgaben, die zur Einführung in die Analysis geeignet sind.
Gegeben sei der Graph einer Funktion f mit 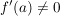 . .
a) Gib die Gleichung der Normalen des Graphen der Funktion f an der Stelle a an.
b) Bestimme die Schnittpunkte dieser Normalen mit den Koordinatenachsen.
c) Wie würde die Normale verlaufen, wenn f'(a) = 0 wäre?
Kann eine ganzrationale Funktion 4. Grades genau eine Berührstelle und genau eine Durchgangsstelle haben?
Für zwei Funktionen 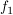 und und 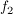 gelte: gelte:
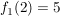 und und 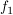 habe dort die Steigung 30° zur x-Achse. habe dort die Steigung 30° zur x-Achse.
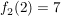 und und 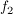 habe dort die Steigung 45° zur x-Achse. habe dort die Steigung 45° zur x-Achse.
Wie lautet die Steigung der Funktion 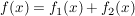 im Punkt x =2? im Punkt x =2?
Bestimme die Gleichung einer Parabel p(x)=ax²+bx+c, die genau eine Nullstelle hat und die die Gerade g(x)=2x+4 bei 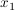 =2 und =2 und 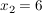 schneidet. schneidet.
Gegeben ist die Funktion f mit 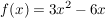
Welche Stammfunktion zu f hat einen Graphen dessen Tiefpunkt auf der x-Achse liegt?
Die Exponentialfunktion 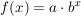 geht durch die Punkte P und Q. Bestimme a und b. geht durch die Punkte P und Q. Bestimme a und b.
a) P (1|6) Q (2|18)
b) P (-1|0,3) Q (2|37,5)
c) P (4|12,5) Q (-1|0,8)
d) P (1/2 | 3) Q (2|18)
Eine Substanz zerfällt so, dass nach jeweils einem Tag 10% [5%] weniger vorhanden ist.
Am Anfang sind 30g vorhanden. Bestimme die Zuordnungsvorschrift.
Wieviel g sind nach 2 Wochen, nach 1 Monat noch vorhanden?
Gegeben: 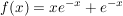
h(x) ist die Umkehrfunktion von f(x)
Begründen Sie, ohne Bestimmung von h(x), an welcher Stelle die Ableitung von h(x) ein lokales Extremum aufweist. Bestimmen Sie den Wert der Ableitung von h(x) an dieser Stelle.
Diese Aufgaben können als Übungsaufgaben verstanden werden;
wenn du die Aufgabe gelöst hast oder noch Fragen dazu stellen möchtest,
poste die Aufgabe und deine Lösungsideen im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) Matheraum. Matheraum.
|