EreignisDefinition Ereignis
Schule
Jede Teilmenge des endlichen Ergebnisraumes 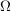 heißt Ereignis A, d.h. heißt Ereignis A, d.h. 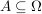 . .
Ein Ereignis 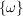 , d.h. eine Teilmenge mit nur einem Ergebnis, heißt Elementarereignis. , d.h. eine Teilmenge mit nur einem Ergebnis, heißt Elementarereignis.
Die Menge aller Ereignisse heißt Ereignisraum 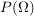 . .
(Das 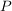 bei bei 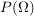 ist dabei eine Abkürzung für die Potenzmenge von ist dabei eine Abkürzung für die Potenzmenge von 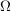 . .
Hier ist also ausnahmsweise mal nicht die Wahrscheinlichkeit gemeint!)
Die Wahrscheinlichkeiten von Ereignissen lassen sich besonders gut berechnen, wenn den Ergebnissen des Zufallsexperiments Zahlen zugeordnet werden: Zufallsgröße
Gegenereignis
Sei E ein Ereignis eines Ergebnisraumes 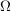 , dann nennt man , dann nennt man 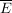 das Gegenereignis zu E bzgl. das Gegenereignis zu E bzgl. 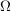 . .
Ergebnisraum und Ereignisse - ein kleines Beispiel
Wir wollen einmal einen Würfel werfen.
Der Ergebnisraum ist 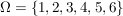 . .
Ein Element 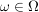 nennt man Ergebnis. nennt man Ergebnis.
Ein Ereignis 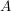 kann man einmal mit Worten formulieren, z.B. "man würfelt eine gerade Zahl", kann man einmal mit Worten formulieren, z.B. "man würfelt eine gerade Zahl",
oder mit der Mengenschreibweise 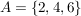 . .
Ein anderes Beispiel wäre das Ereignis 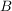 "man würfelt eine Zahl größer als Vier" - das wäre "man würfelt eine Zahl größer als Vier" - das wäre 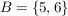 . .
Oder das Ereignis 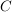 "man würfelt eine Sechs" - das wäre "man würfelt eine Sechs" - das wäre 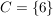 . .
Man kann neue Ereignisse aus den angegebenen Ereignissen bilden:
Oder-Ereignis
"man würfelt eine ungerade Zahl oder man würfelt eine Zahl größer als Vier"
dann bildet man die Vereinigung der beiden Ereignisse: 
Und-Ereignis
"man würfelt eine ungerade Zahl und man würfelt eine Zahl größer als Vier"
insgesamt also: "man würfelt eine ungerade Zahl größer als Vier"
dann bildet man den Durchschnitt der beiden Ereignisse: 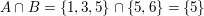
Gegenereignis
"man würfelt nicht eine ungerade Zahl; dann würfelt man eben eine gerade Zahl .."
E={1,3,5} 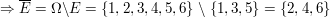
Merke: Ereignisse sind immer Teilmengen des Ergebnisraums!
Man kann für jedes Ereignis die Wahrscheinlichkeit bestimmen -
in den genannten Beispielen wäre 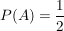 , , 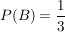 und und 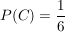 . .
Die Summenregel
Für beliebige Ereignisse 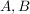 gilt gilt 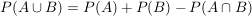 . .
Überprüfen wir die Regel anhand unseres Beispiels: Was ist das Ereignis 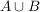 ? ?
In Mengenschreibweise ist 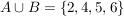 (Vereinigung!) - (Vereinigung!) -
in Worten hieße das "man würfelt eine gerade Zahl oder eine Zahl größer als Vier".
Was ist nun die Wahrscheinlichkeit 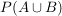 ? ?
Wir können sofort sagen, dass 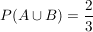 oder aber die Formel benutzen: oder aber die Formel benutzen:
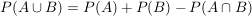 . .
Dazu müssen wir noch wissen, was das Ereignis 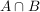 ist, ist,
und wie groß die Wahrscheinlichkeit 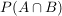 ist... ist...
Es ist 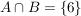 (Schnittmenge!) und damit (Schnittmenge!) und damit 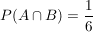 . .
Benutzen wir jetzt die Summenregel:
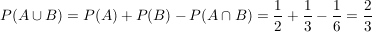 . .
Wir haben damit unsere erste Berechnung bestätigt und dabei (hoffentlich!) gelernt, was es mit der Summenregel auf sich hat.
Universität
|