FunktionentheorieSkript2 §1 Komplexe Zahlen und Polynome §1 Komplexe Zahlen und Polynome  Inhaltsverzeichnis Inhaltsverzeichnis  §3 Komplexes Kurvenintegral §3 Komplexes Kurvenintegral
§2 Komplex differenzierbare Funktionen
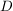 sei offene Teilmenge von sei offene Teilmenge von 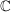 , , 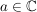 , , 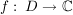 Funktion Funktion
Def 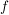 heißt komplex differenzierbar im Punkt heißt komplex differenzierbar im Punkt  , wenn gilt: , wenn gilt:
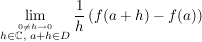 existiert in existiert in 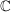 . .
Man nennt dann diesen Grenzwert die komplexe Ableitung von 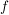 im Punkt im Punkt  und bezeichnet sie oft mit und bezeichnet sie oft mit 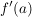 . .
Bem 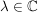
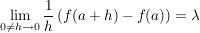 bedeutet: bedeutet:
Ist 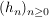 Folge, Folge, 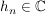 , , 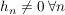 , , 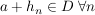 , so ist , so ist 
Übg 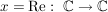
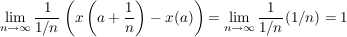
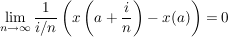
d.h. x ist nicht komplex differenzierbar in 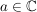 ( (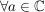 ). ).
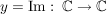
y ist nicht komplex differenzierbar in 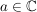 ( (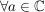 ) )
Übg 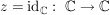
z komplex differenzierbar in a mit 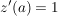 ( (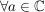 ) )
Es gilt: Es sei 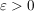 mit mit 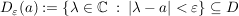
Es sei 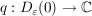
gegeben durch 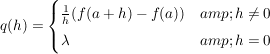
Dann gilt:
 ist stetig. ist stetig.
Es gilt: 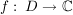 , , 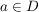 , f komplex differenzierbar in a. , f komplex differenzierbar in a.
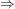 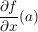 und und 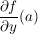 existieren in existieren in 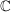 und und

Weiter gilt: 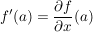 wobei wobei 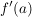 die komplexe Ableitung von f im Punkt a ist. die komplexe Ableitung von f im Punkt a ist.
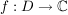
Def f heiße komplex differenzierbar, wenn gilt: 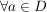 ist f komplex differenzierbar in a[/mm] ist f komplex differenzierbar in a[/mm]
Def Ist f komplex differenzierbat, so ist die komplexe Ableitung f' von f die Funktion, die 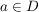 auf f'(a) abbildet (es ist auf f'(a) abbildet (es ist 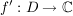 . .
Übg Sei 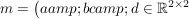 und und 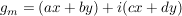
Frage: Für welche m ist 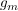 komplex differenzierbar? komplex differenzierbar?
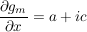 , , 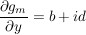
Wenn 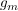 komplex differenzierbar komplex differenzierbar
 (Cauchy-Riemann-Bedingung) (Cauchy-Riemann-Bedingung) 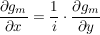
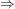 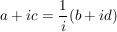
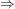 
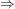 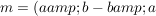
Sei a=d, b=-c
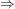 
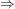 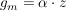 , da (a+ic)(x+iy)=(ax-cy)+i(cx+ay) , da (a+ic)(x+iy)=(ax-cy)+i(cx+ay)
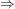 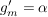
Bsp komplexe Exponentialfunktion
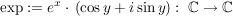
Es gilt: 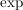 ist komplex differenzierbar. Die komplexe Ableitung ist komplex differenzierbar. Die komplexe Ableitung 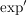 von von 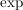 ist ist 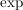 . .
Bsp komplexer Logarithmus
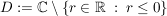
Es gilt: Es existiert eine eindeutig bestimmte Funktion 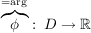 mit mit
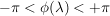 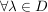
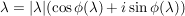
Es sei  gegeben durch gegeben durch 
Es gilt:  ist komplex differenzierbar, ist komplex differenzierbar, 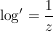
Satz 1 Es seien 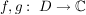 , , 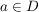
Dann gilt:
(i) Sind f,g komplex differenzierbar in a, so sind
komplex differenzierbar in a und
(ii) Hat f keine Nullstelle in D und ist f komplex differenzierbar in a, so ist 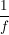 komplex differenzierbar in a und komplex differenzierbar in a und
Übg
![$ f=\summe_{k=0}^{n} a_k z^k\in\IC[z] $ $ f=\summe_{k=0}^{n} a_k z^k\in\IC[z] $](/teximg/8/2/00388628.png) , , 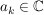
f komplex differenzierbar und die komplexe Ableitung f' ist gleich
Korollar D offen in 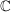 , D zusammenhängend, 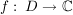 komplex differenzierbar mit f'=0 (f' komplexe Ableitung von f)
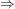 f ist konstante Funktion
Übg Es gibt genau eine komplex differenzierbare Funktion 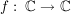 mit mit
(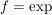 ) )
Übg Es existiert genau eine komplex differenzierbare Funktion  mit mit
(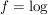 ) )
Bem 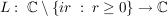 , , 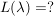
Sei 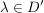
Es existiert genau ein 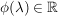 mit: mit:  mit mit 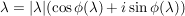
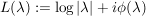
Man kann zeigen: L komplex differenzierbar 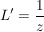
Übg 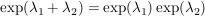 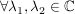
Übg
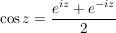

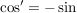

Es sei 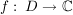 , , 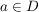
Def f heißt reell differenzierbar in a, wenn gilt:
Es gibt eine reell-lineare Abbdildung 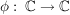 mit: mit: 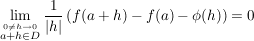
Es gilt: 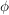 ist durch f und a eindeutig bestimmt und heißt reelle Ableitung ist durch f und a eindeutig bestimmt und heißt reelle Ableitung 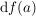 von f in a von f in a
Es gilt: 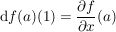 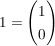
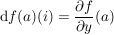 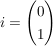
Satz 3 ( Cauchy-Riemann)
Es sei D offen in 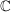 , 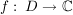 , 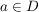
Dann gilt: f komplex differenzierbar in a  f reell differenzierbar und 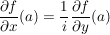
Bem 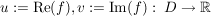

Zusatz zu Satz 3: Ist 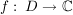 stetig partiell differenzierbar in D (d.h. stetig partiell differenzierbar in D (d.h. 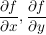 sind stetig in D), so ist f reell differenzierbar in D. sind stetig in D), so ist f reell differenzierbar in D.
Übg 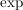 ist komplex differenzierbar ist komplex differenzierbar
Bsp 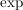 als Abbildung als Abbildung
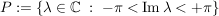
Es gilt: 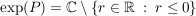
Es gilt:
Es gilt:
Es sei 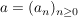 Folge, Folge, 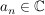
bzw.
Es gilt:  oder es gibt oder es gibt 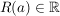 , , 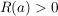 mit mit 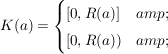
Man setzt 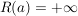 , wenn , wenn 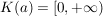 und nennt R(a) den Konvergenzradius von a und nennt R(a) den Konvergenzradius von a
Übg 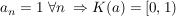
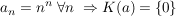
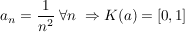
Übg 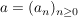 , , 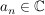
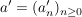 , , 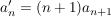
Es gilt: 
^Satz 4 Es sei 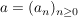 komplexe Zahlenfolge mit komplexe Zahlenfolge mit 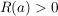 . .
Dann gilt:
(i) Es gibt genau eine Funktion 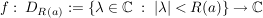 mit: mit:
Ist 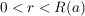 und und 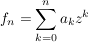 , so konvergiert , so konvergiert 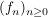 gleichmäßig auf gleichmäßig auf 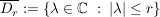 gegen f. gegen f.
Man schreibt 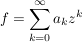
(ii) f ist komplex differenzierbar und 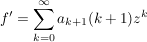
Bem 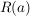 heißt auch Konvergenzradius der formalen Potenzreihe heißt auch Konvergenzradius der formalen Potenzreihe 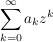
Bsp Sei 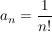 für für 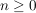
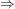 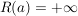
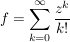 komplex differenzierbare Funktion auf komplex differenzierbare Funktion auf 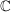 (Satz 4) (Satz 4)
 (Satz 4 (ii)) (Satz 4 (ii))
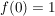 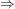 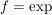
Bsp 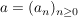 mit mit  für für  , , 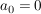
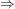 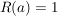
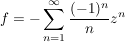 komplex differenzierbar auf komplex differenzierbar auf 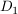
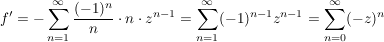
Beh 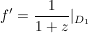
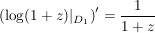 , , 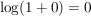 , , 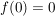 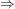 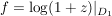
Bem Es sei 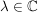 , , 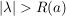
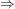 Die Folge Die Folge 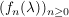 konvergiert nicht in konvergiert nicht in 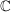
 §1 Komplexe Zahlen und Polynome §1 Komplexe Zahlen und Polynome  Inhaltsverzeichnis Inhaltsverzeichnis  §3 Komplexes Kurvenintegral §3 Komplexes Kurvenintegral
|