Gauß-AlgorithmusGauß-Algorithmus
Sind zwei oder mehr lineare Gleichungen mit zwei oder mehr Unbekannten (= Variablen) gegeben, die gleichzeitig zu lösen sind, spricht man von einem
Linearen Gleichungssystem
Man löst ein lineares Gleichungssystem mit n Variablen, indem man es zunächst mit Hilfe von Äquivalenzumformungen auf Dreiecksform bringt und dann schrittweise nach den Variablen auflöst.
Als Äquivalenzumformungen gelten dabei insbesondere:
- Gleichungen miteinander vertauschen,
- eine Gleichung mit einer Zahl
 multiplizieren, multiplizieren,
- eine Gleichung durch die Summe oder Differenz eines Vielfachen von ihr und einem Vielfachen einer anderen Gleichung ersetzen.
Ziel dieser Umformungen ist es, bei jedem Schritt die Anzahl der Variablen von einer Zeile zur nächsten zu reduzieren.
Beispiel:
(1) 3x + 6y - 2z = -4
(2) 3x + 2y + z = 0
(3) 3x + 10y - 10z = -18
--
(1) 3x + 6y - 2z = -4
(2a)=(2)-(1): -4y + 3z = 4
(3a)=(3)-(1): 4y - 8z = -14
--
(1) 3x + 6y - 2z = -4
(2a)=(2)-(1): -4y + 3z = 4
(3b)=(3a)+(2a): - 5z = -10
--
Nun enthält die Gleichung (3b) nur noch die Variable z, die man berechnen kann: z = 2.
Das Ergebnis setzt man in Gleichung (2a) ein und erhält: y =  . .
Beide Ergebnisse setzt man in (1) ein, um x = -1 zu erhalten.
Lösung ist also das Tripel (x;y;z) = (-1; ; 2). ; 2).
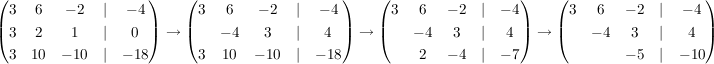
Man erkennt an der Matrix-Schreibweise sehr schön die Dreiecksform, in die das Gleichungssystem umgeformt wird.
Dieses Verfahren läßt sich weitgehend automatisieren, daher ist es auch mit einem Computerprogramm durchzuführen.
Bemerkung
Zum Lösen von linearen Gleichungssystemen mit mehr als 3 Variablen kann man als abkürzende Schreibweise und vereinfachende Rechnungen die Matrixschreibweise und ihren Kalkül benutzen.
|