NormalenformDefinition Normalenform der Ebenengleichung
Schule
Gegeben sei die Ebene E durch 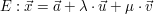 . .
Sei 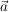 der Ortsvektor zu einem Punkt A der Ebene E, der Ortsvektor zu einem Punkt A der Ebene E,
und sei 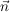 ein Vektor, der auf den Richtungsvektoren ein Vektor, der auf den Richtungsvektoren 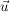 und und 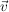 der Ebene (und damit auf der ganzen Ebene) senkrecht steht, dieser Vektor wird Normalenvektor genannt. der Ebene (und damit auf der ganzen Ebene) senkrecht steht, dieser Vektor wird Normalenvektor genannt.
Diesen Normalenvektor kann man mit dem Kreuzprodukt der beiden Spannvektoren relativ schnell ermitteln, es gilt also: 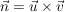
Dann gilt:
oder ausführlich in Koordinatenschreibweise:
oder prägnanter:
Multipliziert man die Skalarprodukte aus, erhält man die Ebenengleichung in Koordinatenform:
mit
Hesse-Form der Ebenengleichung
Benutzt man zum Aufstellen der Normalenform der Ebenengleichung einen Normaleneinheitsvektor
so, dass in der Gleichung
der Ausdruck 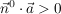 gilt, so heißt diese Normalenform Hesse-Form der Ebenengleichung. gilt, so heißt diese Normalenform Hesse-Form der Ebenengleichung.
Abstandsbetrachtung mit der Hesse-Form:
Setzt man den Ortsvektor 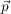 eines Punktes P für eines Punktes P für 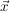 in die Hesse-Form ein, so erhält man die Maßzahl d des Abstands |d| des Punktes P von der Ebene: in die Hesse-Form ein, so erhält man die Maßzahl d des Abstands |d| des Punktes P von der Ebene:
d>0: P und der Ursprung O liegen auf verschiedenen Seiten der Ebene E.
d=0: P liegt auf der Ebene E.
d<0: P und O liegen auf derselben Seite der Ebene E.
Achsenabschnittsform der Ebenengleichung
Sie wird entwickelt aus der Normalenform 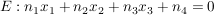 , indem man , indem man 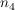 auf die andere Seite der Gleichung holt und anschließend durch auf die andere Seite der Gleichung holt und anschließend durch 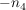 teilt: teilt:
Die Kehrbrüche der Koeffizienten ergeben dann die Spurpunkte der Ebene mit den Koordinatenachsen:
Universität
|