InduktionBeweisverfahren durch vollständige Induktion
Eine Aussage ist gültig für alle natürlichen Zahlen 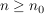 , mit , mit  , wenn man nachweisen kann: , wenn man nachweisen kann:
(I) Die Aussage gilt für die natürliche Zahl  . (Induktionsanfang) . (Induktionsanfang)
(II) Wenn die Aussage für die natürliche Zahl k gilt,
dann gilt sie auch für die nächst höhere Zahl k+1. (Induktionsschritt)
Beispiele
zu zeigen: für alle 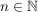 gilt: gilt:  . .
Induktionsanfang:
für n=0 ist die Aussage wahr, denn:  . .
Induktionsschritt:
Es sei jetzt 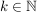 und man nimmt an, dass die Aussage für k gilt: und man nimmt an, dass die Aussage für k gilt:
es gilt also:  . .
Es muss also "nur noch" gezeigt werden, dass
 richtig ist. richtig ist.

Damit ist gezeigt, dass man von einem natürlichen k zum nächst höheren kommt:
also ist die Aussage für alle  wahr. wahr.
Beweisen Sie, dass für alle 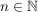 gilt: gilt:  ist durch 133 teilbar ist durch 133 teilbar
Induktionsanfang:
 ist durch 133 teilbar. ist durch 133 teilbar.
Induktionsschritt:
 : :
Zu zeigen ist, dass 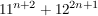 durch 133 teilbar ist. durch 133 teilbar ist.
Es gilt:




Da die letzten beiden Summanden 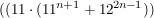 und und 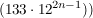
beide durch 133 teilbar sind, sind wir fertig (wegen des Distributivgesetzes!).
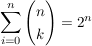
Induktionsanfang:

Induktionsschritt:
Annahme: Diese Aussage ist richtig für 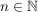 . .
z.z. 
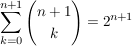
mit 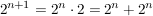
Ziel ist, folgende Gleichheit erkennbar zu machen:
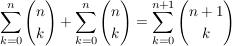
die linke Seite der Gleichung :
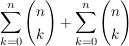
die Summanden für k=0 aus dem ersten Summenzeichen herausziehen, und für k=n aus dem zweiten Summenzeichen.

mit folgender Beziehung macht man eine sogenannte Indexverschiebung...
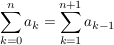
Dann gilt:

Da die Summenzeichen nun über dieselben Indizes laufen, kann man sie zusammenziehen...
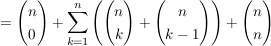
Mit  und und

Letzteres kann man mithilfe der Formeln zur Berechnung des Binomialkoeffizienten nachrechnen
folgt:

Noch'n Trick -

viele Aufgaben zum Üben: ![Link auf "http://mo.mathematik.uni-stuttgart.de/aufgaben/I/induktion__vollstaendige.html" [link]](/images/popup.gif) mo.mathematik.uni-stuttgart.de/aufgaben/I/induktion__vollstaendige.html mo.mathematik.uni-stuttgart.de/aufgaben/I/induktion__vollstaendige.html
|