| Mach mit! und verbessere/erweitere diesen Artikel! | | Artikel • Seite bearbeiten • Versionen/Autoren | MaßDefinition Maß
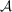 Sigma-Algebra Sigma-Algebra in 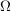 , 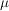 Prämaß auf 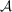
Dann heißt 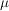 Maß Maß (auf 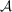 );
für  heißt  das ( 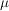 -) Maß der Menge A;
für  heißt 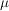 endlich endlich;
falls  heißt 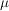 Nullmaß Nullmaß.
Siehe auch: äußeres Maß, Prämaß, Inhalt
Beispiele:
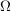 nichtabzählbar (z.B. nichtabzählbar (z.B. ), ),  $\sigma$-Algebra. $\sigma$-Algebra. 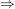  ist Maß auf ist Maß auf 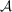 - Dirac-Maß
- Zählmaß
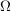 nichtabzählbar (z.B. nichtabzählbar (z.B.  ), ),   -Algebra. -Algebra. 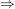  ist Maß auf ist Maß auf 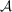 - Lebesgue-Borelsches Maß
- Lebesguesches Maß
Attribute:
Ein Maß 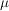 heißt... heißt...
Literatur: isbn3110136252
| | Erstellt: Mo 28.07.2008 von Marc | | Letzte Änderung: Do 02.10.2008 um 23:00 von Marc | | | Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext |
|