MengensystemeVoraussetzungen
 , ,
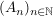 Folge von Mengen aus Folge von Mengen aus 
| Eigenschaft / Mengensystem | Potenz-
menge | Halbring | Ring | Algebra |  -Ring -Ring |  -Algebra -Algebra | Dynkin-
System | |
| 1 |  | ja | ja | ja | ja | ja | ja | ja | |
| 2 |  | ja | ? | nein | ja | nein | ja | ja | |
| 3 |  | ja | ? | ja | ja | ja | ja | nein | |
| 3' |  | ja | ? | ja | ja | ja | ja | ja | |
| 4 |  | ja | ? | nein | ja | nein | ja | ja | |
| 5 |  | ja | ? | ja | ja | ja | ja | ? | |
| 5' |  | ja | ? | ja | ja | ja | ja | ja | |
| 6 |  | ja | ja | ja | ja | ja | ja | nein | |
| 7 |  | ja | ? | ja | ja | ja | ja | ? | |
| 8 |  | ja | ? | nein | nein | ja | ja | ? | |
| 8' |  | ja | ? | nein | nein | ja | ja | ja | |
| 8C'' |  | ja | ? | nein | nein | ja | ja | ja | |
| 9 |  | ja | ? | nein | nein | ja | ja | ? | |
| 9' |  | ja | ? | nein | nein | ja | ja | ja | |
| 10 |  | ja | ? | nein | nein | ja | ja | ? | |
| 11 |  | ja | ? | nein | nein | ja | ja | ? | |
| 12 |  | ja | ? | ? | ? | ? | ? | ja | |
dabei ist:


Falls  monoton wachsend: monoton wachsend: 
Falls  monoton fallend: monoton fallend: 
Definitionen
Halbring: (1), (6), Für alle  gibt es disjunkte gibt es disjunkte  , so dass , so dass 
Ring 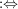 (1), (7), (6) (1), (7), (6)
Ring 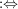 (1), (7), (5) (1), (7), (5)
Ring 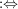 (1), (5), (3) (1), (5), (3)
Algebra 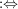 (2), (4), (5) (2), (4), (5)
Algebra 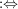 (2), (4), (6) (2), (4), (6)
Algreba 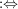 Ring, (2) Ring, (2)
 -Ring -Ring 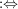 Ring, (8) Ring, (8)
 -Ring -Ring 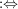 (1), (3), (8) (1), (3), (8)
 -Algebra -Algebra 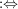  -Ring, (2) -Ring, (2)
 -Algebra -Algebra 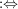 (2), (4), (8) (2), (4), (8)
 -Algebra -Algebra 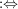 (2), (4), (9) (2), (4), (9)
 -Algebra -Algebra 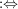 Dynkin-System, (6) Dynkin-System, (6)
Dynkin-System 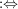 (2), (4), (8') (2), (4), (8')
Dynkin-System 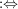 (2), (3'), (12) (2), (3'), (12)
Dynkin-System 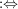 (2), (3'), (8') (2), (3'), (8')
Dynkin-System 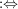 (2), (3'), (8), (9) (2), (3'), (8), (9)
Ein Mengensystem  , das (5) erfüllt, heißt vereinigungsstabil. , das (5) erfüllt, heißt vereinigungsstabil.
Ein Mengensystem  , das (6) erfüllt, heißt durchschnittsstabil. , das (6) erfüllt, heißt durchschnittsstabil.
Zusammenhänge
Algebra 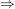 Ring Ring
 -Algebra -Algebra 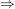 Dynkin-System Dynkin-System
 -Algebra -Algebra 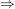 Algebra Algebra 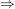 Ring Ring
 -Algebra -Algebra 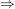  -Ring -Ring 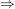 Ring Ring
|