PartialbruchzerlegungEine Partialbruchzerlegung findet häufig Anwendung in Verbindung mit Integralen und Transformationen aus dem Bildbereich.
Auch zur Konvergenz- bzw. Grenzwertbestimmung von Folge- und Reihengliedern kann man des öfteren diese Methode als Lösungsweg nehmen.
Zu Beginn betrachten wir allgemein eine gebrochen-rationale Funktion in x der Form  mit dem Zählerpolynom mit dem Zählerpolynom 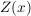 und dem Nennerpolynom und dem Nennerpolynom 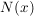
Es ist hier jedoch schon zu prüfen, ob eine echt gebrochen-rationale Funktion vorliegt, das heißt, dass der Grad des Zählerpolynoms 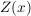 kleiner als jener des Nennerpolynoms kleiner als jener des Nennerpolynoms 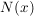 sein soll. Ist dies nicht der Fall, dann muss sein soll. Ist dies nicht der Fall, dann muss 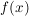 erst in diese Form gebracht werden; z.B. mit einer Polynomdivision. erst in diese Form gebracht werden; z.B. mit einer Polynomdivision.
Der echt gebrochen-rationale Term kann mit algebraischen Mittel dann in Teilbrüche, die sogenannten Partialbrüche, zerlegt werden. Ich führe hier einige Methoden an.
Zunächst müssen die Nullstellen des Nenners ermittelt werden, da für jede Nullstelle ein Partialbruch generiert wird.
Dieses stellt sich wie folgt dar:

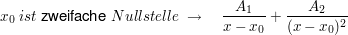

Allgemeine Beschreibung:
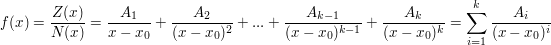
Beispiel (gleiche Nullstellen):  ist 2-fache Nullstelle: ist 2-fache Nullstelle:

Beispiel (unterschiedliche Nullstellen):  ist 2-fache Nullstelle und ist 2-fache Nullstelle und 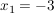 ist 1-fache Nullstelle: ist 1-fache Nullstelle:
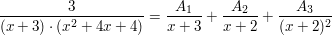
Nun werden die Brüche auf den gemeinsamen Nenner erweitert und ein Koeffizientenvergleich durchgeführt oder es kann nach dem Einsetzen verschiedener Nullstellen der Gauß-Algorithmus angewendet werden.
Eine weitere Lösungsmöglichkeit bietet das Verfahren nach Heaviside
Hier folgt nun ein Beispiel zur Veranschaulichung:
Es soll das unbestimmte Integral 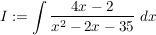 vereinfacht werden. Für die Vereinfachung benötigen wir die Nullstellen des Nenners: vereinfacht werden. Für die Vereinfachung benötigen wir die Nullstellen des Nenners:
Unter Verwendung der p-q-Formel erhält man für 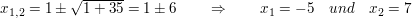
Der Integrand lässt sich dann in der folgenden Form darstellen

Erweiterung auf den Hauptnenner und Betrachten der beiden Zähler:
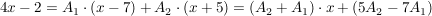
Koeffizientenvergleich
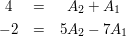
Nach dem Einsetzverfahren wird für 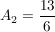 und für und für  ermittelt ermittelt
So lässt sich das Integral in die Teilintegrale zerlegen

und als Ergebnis kann
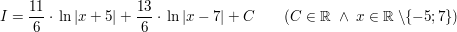
mit Kenntnissen der Integrationsregeln unmittelbar abgelesen werden.
Komplexe Nullstellen
Bei Polynomen mit reellen Koeffizienten können neben den reellen Lösungen auch Lösungen aus den komplexen Zahlen vorliegen. Diese treten dann jeweils konjugiert komplex auf. Nach oben angegeben Schema würde eine Partialbruchzerlegung wie folgt aussehen
Die Funktion  besitzt im Nennerpolynom neben der reellen Nullstelle besitzt im Nennerpolynom neben der reellen Nullstelle 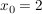
zwei weitere komplexe Lösungen 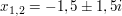
![$ f(x)=\bruch{1}{2}\cdot{}\bruch{3x^2+3x-6}{x^3+x^2-1,5x-9}=\bruch{1}{2}\cdot{}\left[\bruch{A}{x+1,5+1.5i}+\bruch{B}{x+1,5-1,5i}+\bruch{C}{x-2}\right] $ $ f(x)=\bruch{1}{2}\cdot{}\bruch{3x^2+3x-6}{x^3+x^2-1,5x-9}=\bruch{1}{2}\cdot{}\left[\bruch{A}{x+1,5+1.5i}+\bruch{B}{x+1,5-1,5i}+\bruch{C}{x-2}\right] $](/teximg/4/6/01280164.png)
Hier bietet sich jedoch ein weitere möglicher Ansatz mit
![$ f(x)=\bruch{1}{2}\cdot{}\bruch{3x^3+3x-6}{x^3+x^2-1,5x-9}=\bruch{1}{2}\cdot{}\left[\bruch{Ax+B}{x^2+3x+4,5}+\bruch{C}{x-2}\right] $ $ f(x)=\bruch{1}{2}\cdot{}\bruch{3x^3+3x-6}{x^3+x^2-1,5x-9}=\bruch{1}{2}\cdot{}\left[\bruch{Ax+B}{x^2+3x+4,5}+\bruch{C}{x-2}\right] $](/teximg/5/6/01280165.png)
Somit wird bereits im Ansatz eine komplexe Darstellung umgangen.
Verallgemeinerung
Sei 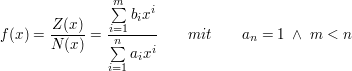
Unter der Voraussetzung, dass
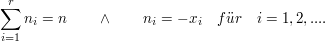
lässt sich das Nennerpolynom N(x) als Produkt darstellen
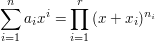
Die zugehörige Partialbruchzerlegung lautet nun:
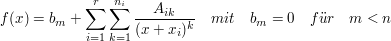
Die Koeffizienten 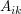 lassen sich über den Entwicklungssatz nach Heaviside bestimmen. lassen sich über den Entwicklungssatz nach Heaviside bestimmen.
zur MatheBank
|