FormvariablenFunktionen mit Formvariablen
Schule
Führt man in die Funktionsgleichung einer Elementarfunktion eine Konstante als Formvariable ein, so erhält man eine Verschiebung oder eine Streckung, bei mehreren Formvariablen eine Kombination dieser Abbildungen.
Verschiebung um d in y-Richtung: 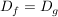
Verschiebung nach oben für d>0; Verschiebung nach unten für d<0.
Multiplikation aller Funktionswerte mit 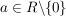 : :
Streckung für a > 1; Stauchung für 0<a<1; keine Änderung für a=1.
Verschiebung um c in x-Richtung, 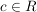
Verschiebung nach links für c < 0; Verschiebung nach rechts für c > 0.
Strecken mit Faktor b in x-Richtung, 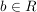
Streckung für b < 1; Stauchung für 0<b<1; keine Änderung für b=1.
Wenn alle diese Formvariablen zusammen wirken, ergibt sich eine Funktion g
Bemerkungen:
- Die Klammersetzung beeinflusst die Reihenfolge einiger dieser Verschiebungen/Streckungen und sollte daher gut bedacht sein!
- Man benötigt solche Überlegungen, um eine weniger bekannte Funktion auf eine besser bekannte Funktion zurückzuführen: dadurch kann man sich schneller einen Überblick über den Verlauf der unbekannten Funktion verschaffen.
Statt 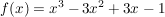 zu untersuchen, stellt man fest, dass zu untersuchen, stellt man fest, dass 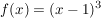 gilt und dass diese Funktion aus der Funktion gilt und dass diese Funktion aus der Funktion 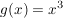 durch eine Verschiebung um 1 nach rechts hervorgegangen ist. durch eine Verschiebung um 1 nach rechts hervorgegangen ist.
f hat daher Nullstelle und Sattelpunkt bei x=1, ohne weiteren größeren Nachweis.
Beispiel für horizontale Streckung
Stauchung:
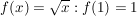
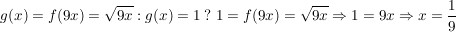
Statt an der Stelle x=1 wird nun der Wert schon an der Stelle 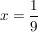 erreicht, also weiter links, der Graph ist also mit dem Faktor erreicht, also weiter links, der Graph ist also mit dem Faktor  gestaucht worden. gestaucht worden.
Streckung:
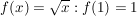
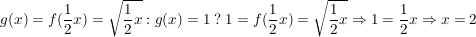
Statt an der Stelle x=1 wird nun der Wert erst an der Stelle x=2 erreicht, also weiter rechts, der Graph ist also mit dem Faktor 2 gestreckt worden.
Am Bild kannst du allerdings auch erkennen, dass die Streckung/Stauchung als Stauchung/Streckung in y-Richtung interpretiert werden kann:
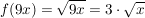
|