direktes Produkt von MengenDefinition direktes Produkt von Mengen
Schule
Universität
Ist 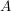 eine nichtleere Menge und eine nichtleere Menge und 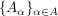 eine Familie von Mengen, dann heißt die Menge eine Familie von Mengen, dann heißt die Menge

das direkte (oder cartesische) Produkt der Mengen 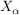 , , 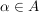 . .
Für eine endliche Indexmenge, z.B. 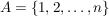 , schreibt man , schreibt man
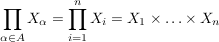 . .
In Übereinstimmung mit den  -Tupeln schreibt man auch bei beliebigem -Tupeln schreibt man auch bei beliebigem 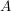 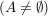 die Elemente die Elemente 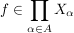 in der Form in der Form 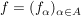 . Hierin ist . Hierin ist 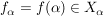 gemeint. gemeint.
Quelle: isbn3446130799
|