e-Funktion AufgabeQuelle: hier und hier
Für jedes t > 0 ist eine Funktion 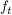 gegeben durch gegeben durch
Der Graph von 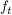 sei sei 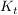 . .
a) Untersuchen Sie 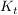 auf Schnittpunkte mit der x - Achse, auf Hoch-, Tief- und Wendepunkte sowie auf Schnittpunkte mit der x - Achse, auf Hoch-, Tief- und Wendepunkte sowie
auf Asymptoten. Zeichen Sie 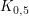 für für 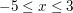 . (Längeneinheit 1 cm) . (Längeneinheit 1 cm)
b) Es sei S der Schnittpunkt der Kurve 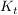 mit der y-Achse. Die Kurventangente in S, die mit der y-Achse. Die Kurventangente in S, die
Kurvennormale in S und die x - Achse bilden ein Dreieck.
Für welchen Wert von t wird der Flächeninhalt dieses Dreiecks am kleinsten?
Zeigen Sie, dass das Dreieck mit dem kleinsten Inhalt gleichschenklig ist.
c ) Die x - Achse und die Kurve 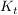 begrenzen eine längs der negativen x - Achse ins Unendliche begrenzen eine längs der negativen x - Achse ins Unendliche
reichende Fläche.
Zeigen Sie, dass die Gerade y = 3 diese Fläche in einem von t unabhängigen Verhältnis teilt.
d) Zu jedem t > 0 ist eine Funktion 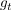 gegeben durch gegeben durch 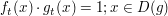 . .
Bestimmen Sie den maximalen Definitionsbereich D(g).
Der Graph von 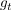 sei sei 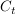 . .
Bestimmen Sie die Anzahl der gemeinsamen Punkte von 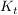 und und 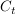 . .
Es sei u eine für alle 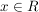 differenzierbare Funktion mit differenzierbare Funktion mit  für alle für alle 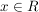 . .
Die Funktion v ist für alle 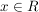 definiert durch u(x)*v(x) = 1. definiert durch u(x)*v(x) = 1.
Zeigen Sie, dass u'(x)*v'(x) für alle 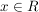 nicht positiv ist. nicht positiv ist.
|