GeradeDefinition Gerade
- Graph einer linearen Funktion
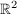 oder oder 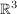 : Menge von Punkten, die durch einen Punkt und einen Vektor (eine Richtung) beschrieben wird. : Menge von Punkten, die durch einen Punkt und einen Vektor (eine Richtung) beschrieben wird.
Schule
- Gerade heißt der Graph einer linearen Funktion.
Sei 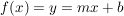 eine lineare Funktion. Diese Form der Geradengleichung im eine lineare Funktion. Diese Form der Geradengleichung im 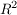 nennt man die Normalform. nennt man die Normalform.
Ihr Graph ist eine Gerade, die die Steigung 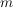 hat und die y-Achse bei hat und die y-Achse bei 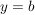 , dem Achsenabschnitt schneidet. , dem Achsenabschnitt schneidet.
siehe auch: Geraden im 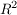 : Geradengleichung : Geradengleichung
Für jede reelle Zahl 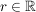 erhält man einen Punkt P, der auf der Geraden liegt und umgekehrt: zu jedem Geradenpunkt gibt es ein erhält man einen Punkt P, der auf der Geraden liegt und umgekehrt: zu jedem Geradenpunkt gibt es ein 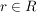 , das die Gleichung erfüllt. , das die Gleichung erfüllt.
Dabei spielt es keine Rolle, ob die angesprochenen Vektoren zwei- oder dreidimensional sind.
In der Regel benutzt man die Vektorgleichungen allerdings meistens für Geraden im Raum 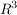 . .
Verläuft eine Gerade durch zwei Punkte A und B,
so erhält man die Zwei-Punkte-Form der Geradengleichung:
in Vektorform:
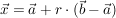 mit 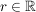
in Koordinatenform (nur im 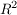 ): ):
Bemerkung
Eine Gerade ist durch einen Punkt und eine Richtung eindeutig bestimmt.
Die Richtung kann auch durch zwei Punkte und deren Verbindungsvektor festgelegt sein.
Da die Geradengleichung den Parameter r enthält, nennt man diese auch Geradengleichung in Parameterform.
Universität
|